静态分析笔记
一、程序的表示¶
1.1 概述¶
- Definition: 静态分析(Static Analysis) 是指在实际运行程序 \(P\) 之前,通过分析静态程序 \(P\) 本身来推测程序的行为,并判断程序是否满足某些特定的 性质(Property) \(Q\)
Rice定理(Rice Theorem):对于使用 递归可枚举(Recursively Enumerable) 的语言描述的程序,其任何 非平凡(Non-trivial) 的性质都是无法完美确定的。
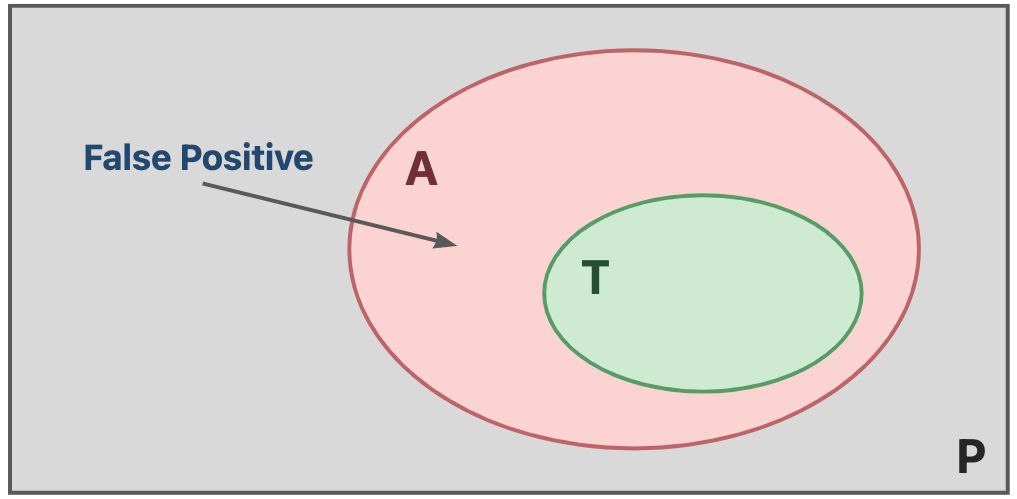
由上可知不存在完美的程序分析,要么满足完全性(Soundness),要么满足正确性(Completeness)。Sound 的静态分析保证了完全性,妥协了正确性,会过近似(Overapproximate)程序的行为,因此会出现假阳性(False Positive)的现象,即误报问题。现实世界中,Sound的静态分析居多,因为误报可以被暴力排查,而Complete的静态分析存在漏报,很难排查。
Static Analysis: ensure (or get close to) soundness, while making good trade-offs between analysis precision and analysis speed.
两个词概括静态分析:抽象,过近似
过近似上文已经提到过了,这里说明一下抽象,即将具体值转化为符号值。例如将如下表左侧具体值转化为右侧抽象符号
| 具体值 | 抽象值 |
|---|---|
| v = 1000 | + |
| v = -1 | - |
| v = 0 | 0 |
| v = x ? 1 : -1 | (丅)unknown |
| v = w / 0 | (丄)undefined |
接下来就可以设计转移方程( Transfer functions),即在抽象值上的操作
再看一个例子,体会一下 Sound 的,过近似的分析原则:
1 2 3 4 5 6 | |
我们会发现,在进入 2-5 行的条件语句的时候, \(y\) 的值可能为 \(10\) ,也可能为 \(-1\) ,于是,我们最终会认为y的抽象值为 \(\top\) ,最终 \(z\) 的抽象值也就为 \(\top\) ,这样,我们的分析就是尽可能全面的,虽然它并不精确。
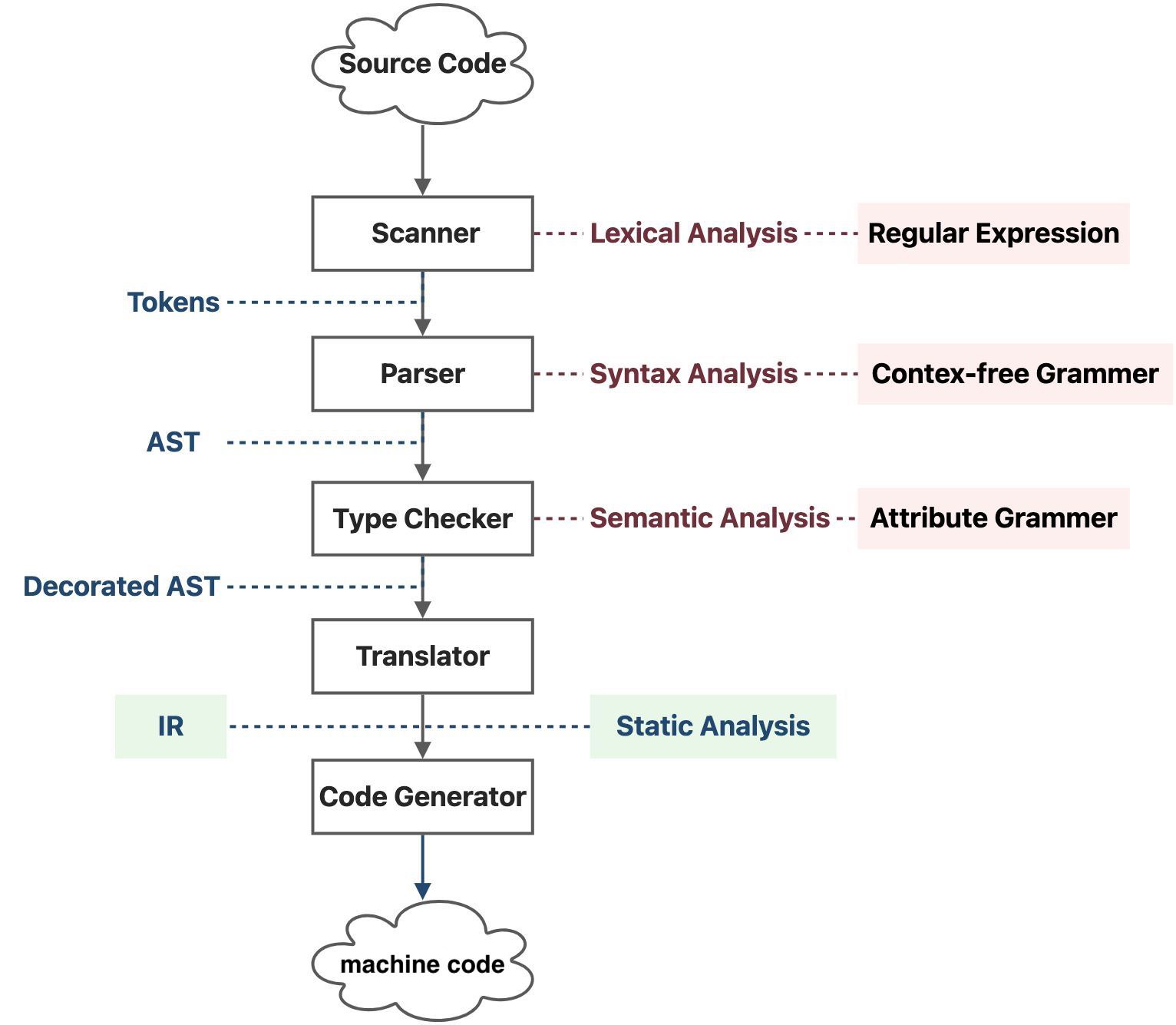
1.2 中间表示¶
编译器和静态分析器¶
静态分析一般发生在 IR 层
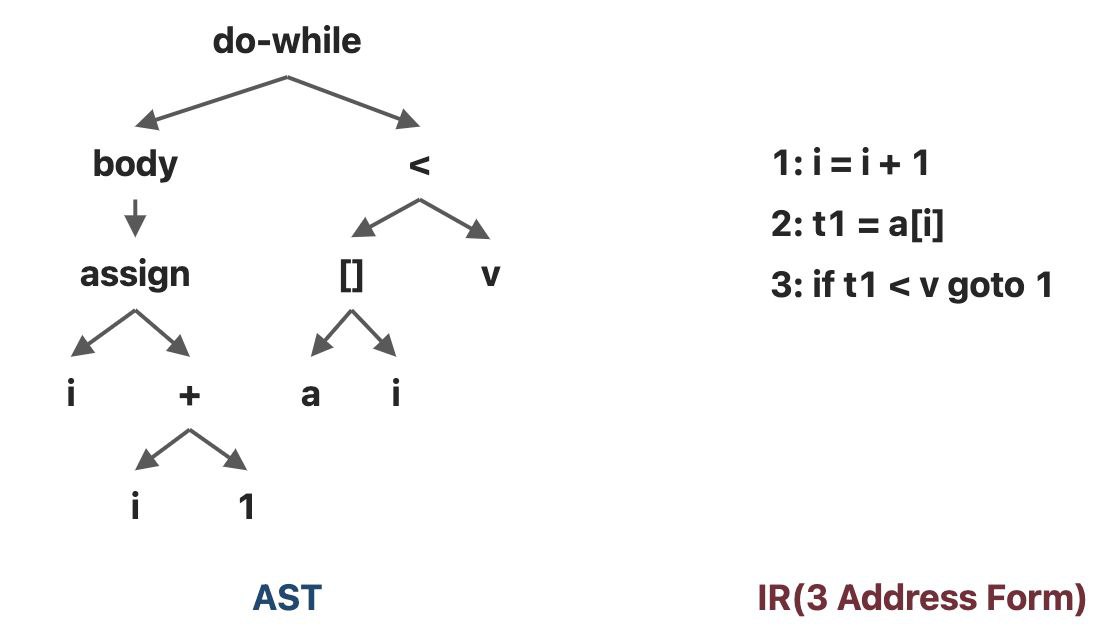
考虑下面一小段代码:
1 | |
AST和三地址码 IR 如下
| AST | IR |
|---|---|
| 层次更高,和语法结构更接近 | 低层次,和机器代码相接近 |
| 通常是依赖于具体的语言类的 | 通常和具体的语言无关,主要和运行语言的机器(物理机或虚拟机)有关 |
| 适合快速的类型检查 | 简单通用 |
| 缺少和程序控制流相关的信息 | 包含程序的控制流信息 |
| 通常作为静态分析的基础 |
-
Definition: 我们将形如 \(f(a_1, a_2, ..., a_n)\) 的指令称为 \(n\) 地址码(N-Address Code),其中,每一个 \(a_i\) 是一个地址,既可以通过 \(a_i\) 传入数据,也可以通过 \(a_i\) 传出数据, \(f\) 是从地址到语句的一个映射,其返回值是某个语句 \(s\) , \(s\) 中最多包含输入的 \(n\) 个地址。这里,我们定义某编程语言 \(L\) 的语句 \(s\) 是 \(L\) 的操作符、关键字和地址的组合。
-
3地址码(3-Address Code,3AC),每条 3AC 至多有三个地址。而一个「地址」可以是:名称 Name:,例如a, b;常量 Constant,例如 3;编译器生成的临时变量 Compiler-generated Temporary,例如
t1,t2
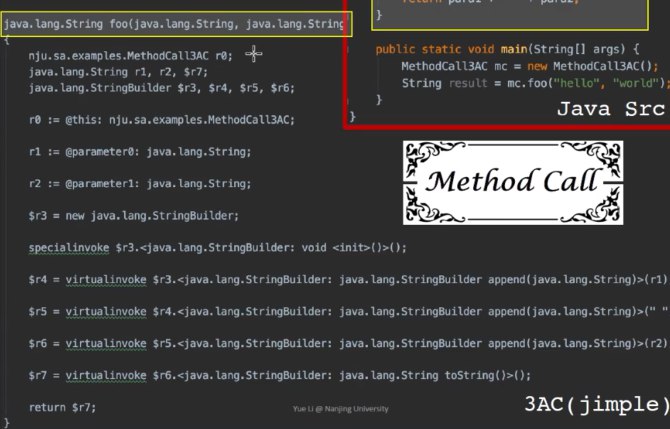
以Soot与它的 IR 语言 Jimple为例
1 2 3 4 5 6 7 8 9 10 11 | |
- 静态单赋值(Static Single Assignment,SSA) 是另一种IR的形式,它和3AC的区别是,在每次赋值的时候都会创建一个新的变量,也就是说,在SSA中,每个变量(包括原始变量和新创建的变量)都只有唯一的一次定义。
控制流分析¶
- 基块
控制流分析(Control Flow Analysis, CFA) 通常是指构建 控制流图(Control Flow Graph,CFG) 的过程。CFG是我们进行静态分析的基础,控制流图中的结点可以是一个指令,也可以是一个基块(Basic Block)。
简单来讲,基块就是满足两点的最长的指令序列:第一,程序的控制流只能从首指令进入;第二,程序的控制流只能从尾指令流出。构建基块的算法如下
- 找到所有的leaders:程序的入口为leader;跳转的target为leader;跳转语句的后一条语句为leader
- 以leader为分割点取最大集
- 控制流图 CFG
构建算法如下
- 对所有最后一条语句不是跳转的basic block与其相邻的basic block相连
- 对有最后一条语句是有条件跳转的basic block,与其相邻的basic block和其跳转的basic block相连
- 对于最后一条语句是无条件跳转的basic block,直接将其于跳转的basic block相连
此外,对于控制流图来说还有两个概念Entry 和 Exit
- Entry即程序的入口,通常是第一个语句,一般来说只有一个
- Exit则是程序的出口,通常是return之类的语句,可能会有多个
二、数据流分析与应用¶
数据流分析——应用¶
数据流分析初步¶
- Definition: 数据流分析(Data Flow Analysis, DFA) 是指分析“数据在程序中是怎样流动的”。具体来讲,其 分析的对象是基于抽象(概述中提到)的应用特定型数据(Application-Specific Data) ;分析的行为是数据的“流动(Flow)”,分析的方式是 安全近似(Safe-Approximation),即根据安全性需求选择过近似(Over-Approximation)还是欠近似(Under-Approximation);分析的基础是控制流图(Control Flow Graph, CFG),CFG是程序 \(P\) 的表示方法;
数据流动的场景有两个:
- Transfer function:在CFG的点(Node)内流动,即Basic block内部的数据流;
-
Control-flow handling:在CFG的边(Edge)上流动,即由基块间控制流触发的数据流。
-
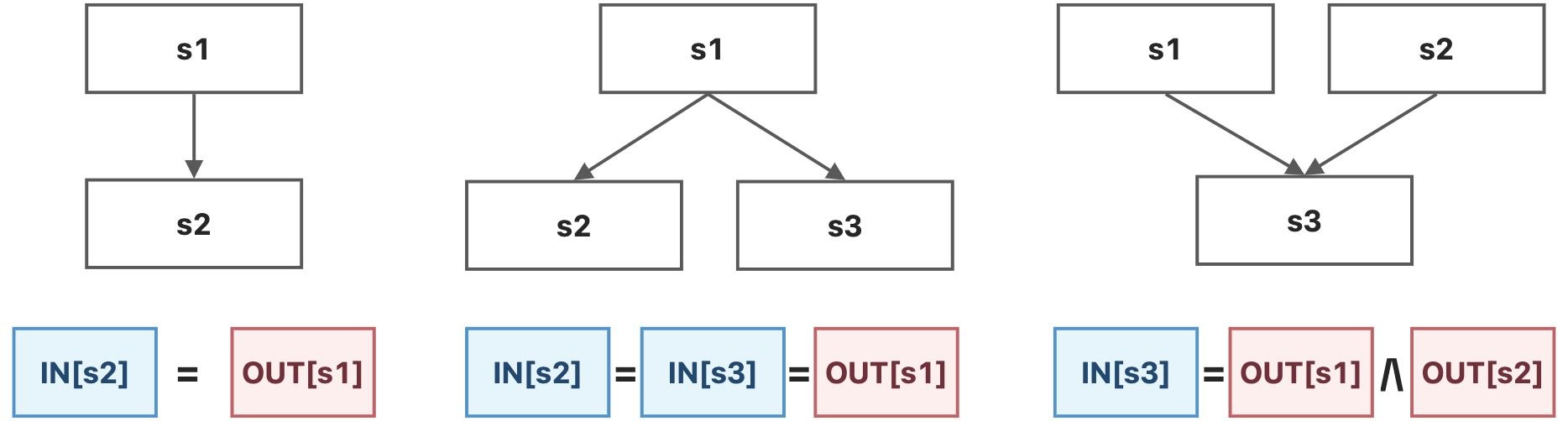
输入输出状态
现在,我们能够定义,数据流分析就是要寻找一种解决方案(即 \(f_{pp}->D\) ),对于程序 \(P\) 中的所有语句 \(s\) ,这种解决方案能够满足 \(IN[s]\) 和 \(OUT[s]\) 所需要满足的安全近似导向型约束(Safe-Approximation-Oriented Constraints, SAOC),SAOC主要有两种:
- 基于语句语意(Sematics of Statements)的约束,即由状态转移方程产生的约束;
- 基于控制流(Flow of Control)的约束,即上述输入输出状态所产生的约束。
定义可达性分析¶
- 当前阶段假设程序中不存在method call
-
当前阶段假设程序中不存在aliaes,别名
-
Definition: 我们称在程序点 \(p\) 处的一个定义 \(d\) 到达(Reach) 了程序点 \(q\) ,如果存在一条从 \(p\) 到 \(q\) 的“路径”(控制流),在这条路径上,定义 \(d\) 未被 覆盖(Kill) 。称分析每个程序点处能够到达的定义的过程为 **定义可达性分析(Reaching Definition Analysis) **
从上面的定义中我们可以看出,“定义可达性”其实描述了一个定义可能的最长的生存期(Lifetime),因为如果存在只要一条路径,我们就认为可达,这是一个可能性分析(May Analysis),采用的是过近似(Over-Approximation)的原则。
三、指针分析与应用¶
四、技术拓展¶
TODO
创建日期: 2024-06-26